Hearing the shape of a drum
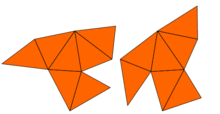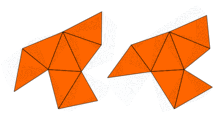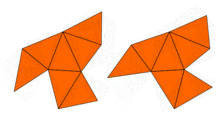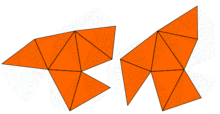
The question of whether the frequencies determine the shape was finally answered in the negative in the early 1990s by Carolyn S. Gordon, David Webb and Scott A. Wolpert.The term "homophonic" is justified because the Dirichlet eigenvalues are precisely the fundamental tones that the drum is capable of producing: they appear naturally as Fourier coefficients in the solution wave equation with clamped boundary.In 1964, John Milnor observed that a theorem on lattices due to Ernst Witt implied the existence of a pair of 16-dimensional flat tori that have the same eigenvalues but different shapes.However, the problem in two dimensions remained open until 1992, when Carolyn Gordon, David Webb, and Scott Wolpert constructed, based on the Sunada method, a pair of regions in the plane that have different shapes but identical eigenvalues.On the other hand, Steve Zelditch proved that the answer to Kac's question is positive if one imposes restrictions to certain convex planar regions with analytic boundary.It is also known, by a result of Osgood, Phillips, and Sarnak that the moduli space of Riemann surfaces of a given genus does not admit a continuous isospectral flow through any point, and is compact in the Fréchet–Schwartz topology.

eigenfrequenciesdrumheadovertonesmathematicalMark KacAmerican Mathematical MonthlyLipman BersArthur SchusterLester R. Ford AwardChauvenet PrizeHelmholtz equationeigenvaluesLaplacianReuleaux triangleCarolyn S. GordonDavid WebbScott A. WolpertdomainDirichlet eigenvaluesDirichlet problemisospectralFourier coefficientswave equationRiemannian manifoldselliptic differential operatorsCauchy–Riemann operatorDirac operatorNeumann boundary conditionspectral geometryJohn MilnorErnst WittCarolyn GordonScott WolpertSunada methodconcave polygonsSteve ZelditchconvexanalyticCheng's eigenvalue comparison theoremRiemann surfacesWeyl lawVictor IvriiMichael BerryHausdorff dimensionupper box dimensionPomeranceGassmann tripleVibrations of a circular membraneKac, MarkNotices of the AMSBibcodeBuser, PeterConway, JohnInternational Mathematics Research NoticesThas, KoenGordon, CarolynWebb, DavidAmerican ScientistGordon, C.Webb, D.RussianRiemann hypothesis"The Riemann zeta-function and the one-dimensional Weyl-Berry conjecture for fractal drums"CiteSeerXPomerance, CarlMathematical Proceedings of the Cambridge Philosophical SocietyMilnor, JohnSunada, T.John Horton ConwayWeisstein, Eric W.MathWorldEncyclopedia of MathematicsEMS Press