Knot (mathematics)
Framed links are said to be equivalent if their extensions to solid tori are ambient isotopic.Replacing the type I move by a modified type I move gives a result for link diagrams with blackboard framing similar to the Reidemeister theorem: Link diagrams, with blackboard framing, represent equivalent framed links if and only if they are connected by a sequence of (modified) type I, II, and III moves.[9] The framing in this sense is associated to the number of twists the vector field performs around the knot.Knowing how many times the vector field is twisted around the knot allows one to determine the vector field up to diffeomorphism, and the equivalence class of the framing is determined completely by this integer called the framing integer.Aaron Trautwein compiled parametric representations for all knots up to and including those with a crossing number of 8 in his PhD thesis.We construct a new plane graph whose vertices are the white faces and whose edges correspond to crossings.[18] In contemporary mathematics the term knot is sometimes used to describe a more general phenomenon related to embeddings.[21] Alexander's theorem states that the 2-sphere does not smoothly (or PL or tame topologically) knot in the 3-sphere.[22] In the tame topological category, it's known that the n-sphere does not knot in the n + 1-sphere for all n. This is a theorem of Morton Brown, Barry Mazur, and Marston Morse.The case n = 3 is a long-outstanding problem closely related to the question: does the 4-ball admit an exotic smooth structure?If one allows topological or PL-isotopies, Christopher Zeeman proved that spheres do not knot when the co-dimension is greater than 2.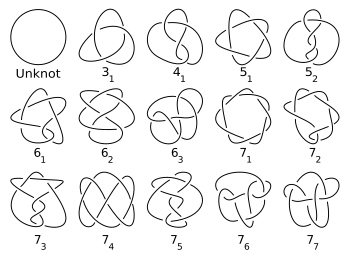












Knot (disambiguation)prime knotscrossingsoverhand knottrefoil knotPretzelpretzel knotmathematicsembeddingEuclidean spaceambient isotopicknot theorygraph theorycirclethree-dimensional3-spherecompactambient isotopysphereinjectivecollinearisotopyknot diagramplanar graphReidemeister movesunknotfigure-eight knotcinquefoil knotfinite setline segmentspathological3-manifoldsolid toruslinking numberintegerReidemeister moveknot complementtheorem of Gordon and Luecke3-manifold theoryJSJ decompositionThurston's hyperbolization theoremsatellite operationstrefoil complementsBorromean ringsknot diagramsmedial graphPeter Taitplane graphhomeomorphicJordan curve theoremthe knot in a mirrorlinkless embeddingPetersen familyplanar graphsundirected graphlinkless embeddingsknotless embeddingsunlinkedunknottedforbidden graph characterizationcomplete graphSchoenflies theoremAlexander's theoremMorton BrownBarry MazurMarston MorseAlexander horned sphereexotic smooth structureAndré HaefligercodimensionStephen Smaleh-cobordism theoremChristopher ZeemanKnot invariantList of mathematical knots and linksone-point compactificationclosed polygonal chainKauffman, Louis H.Transactions of the American Mathematical SocietyProQuestTait, Peter G.Robertson, NeilSeymour, PaulThomas, RobinAlexander, J. W.Proceedings of the National Academy of Sciences of the United States of AmericaBibcodeUndergraduate Texts in MathematicsThe Knot AtlasHyperbolicFigure-eightThree-twistStevedoreEndlessCarrick matPerko pairConway knotKinoshita–Terasaka knot(−2,3,7) pretzelWhiteheadL10a140SatelliteComposite knotsGrannySquareKnot sumTrefoilCinquefoilSeptafoilUnlinkSolomon'sInvariantsAlternatingArf invariantBridge no.2-bridgeBrunnianChiralityInvertibleCrosscap no.Crossing no.Finite type invariantHyperbolic volumeKhovanov homologyKnot groupLink group