Syllogism
A syllogism (Ancient Greek: συλλογισμός, syllogismos, 'conclusion, inference') is a kind of logical argument that applies deductive reasoning to arrive at a conclusion based on two propositions that are asserted or assumed to be true.In its earliest form (defined by Aristotle in his 350 BC book Prior Analytics), a deductive syllogism arises when two true premises (propositions or statements) validly imply a conclusion, or the main point that the argument aims to get across.Within some academic contexts, syllogism has been superseded by first-order predicate logic following the work of Gottlob Frege, in particular his Begriffsschrift (Concept Script; 1879).The onset of a New Logic, or logica nova, arose alongside the reappearance of Prior Analytics, the work in which Aristotle developed his theory of the syllogism.Prior Analytics, upon rediscovery, was instantly regarded by logicians as "a closed and complete body of doctrine", leaving very little for thinkers of the day to debate, and reorganize.Aristotle's theory on the syllogism for assertoric sentences was considered especially remarkable, with only small systematic changes occurring to the concept over time.His original assertions on this specific component of the theory were left up to a considerable amount of conversation, resulting in a wide array of solutions put forth by commentators of the day.The system for modal syllogisms laid forth by Aristotle would ultimately be deemed unfit for practical use, and would be replaced by new distinctions and new theories altogether.While his Latin translation of Prior Analytics went primarily unused before the 12th century, his textbooks on the categorical syllogism were central to expanding the syllogistic discussion.Rather than in any additions that he personally made to the field, Boethius' logical legacy lies in his effective transmission of prior theories to later logicians, as well as his clear and primarily accurate presentations of Aristotle's contributions.The French philosopher Jean Buridan (c. 1300 – 1361), whom some consider the foremost logician of the later Middle Ages, contributed two significant works: Treatise on Consequence and Summulae de Dialectica, in which he discussed the concept of the syllogism, its components and distinctions, and ways to use the tool to expand its logical capability.In the 17th century, Francis Bacon emphasized that experimental verification of axioms must be carried out rigorously, and cannot take syllogism itself as the best way to draw conclusions in nature.[9] Bacon proposed a more inductive approach to the observation of nature, which involves experimentation, and leads to discovering and building on axioms to create a more general conclusion.The work of Bolzano had been largely overlooked until the late 20th century, among other reasons, because of the intellectual environment at the time in Bohemia, which was then part of the Austrian Empire.The Aristotelian system is explicated in modern fora of academia primarily in introductory material and historical study.One notable exception to this modern relegation is the continued application of Aristotelian logic by officials of the Congregation for the Doctrine of the Faith, and the Apostolic Tribunal of the Roman Rota, which still requires that any arguments crafted by Advocates be presented in syllogistic format.The differing positions of the major, minor, and middle terms gives rise to another classification of syllogisms known as the figure.Putting it all together, there are 256 possible types of syllogisms (or 512 if the order of the major and minor premises is changed, though this makes no difference logically).All but four of the patterns in italics (felapton, darapti, fesapo and bamalip) are weakened moods, i.e. it is possible to draw a stronger conclusion from the premises.To argue that its validity can be explained by the theory of syllogism would require that we show that Socrates is a man is the equivalent of a categorical proposition.If AaB and AeB is a fair representation of the use of statements in normal natural language of All A is B and No A is B respectively, then the following example consequences arise: If it is ruled that no universal statement has existential import then the square of opposition fails in several respects (e.g. AaB does not entail AiB) and a number of syllogisms are no longer valid (e.g. BaC, AaB->AiC).The first-order predicate calculus avoids such ambiguity by using formulae that carry no existential import with respect to universal statements.Thus, natural language statements—of the forms All A is B, No A is B, Some A is B, and Some A is not B—can be represented in first order predicate calculus in which any existential import with respect to terms A and/or B is either explicit or not made at all.Because of this, it can be hard to follow formal logic, and a closer eye is needed in order to ensure that an argument is, in fact, valid.
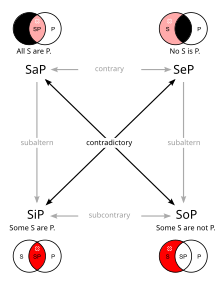
(Black areas are empty,
red areas are nonempty.)
























Epagoge (moth)Minor Premise (film)Ancient Greeklogical argumentdeductive reasoningconclusionpropositionsAristotlePrior AnalyticsSocratesAristotelian syllogismStoic syllogismMiddle Agesinductive reasoningfirst-order predicate logicGottlob FregeBegriffsschriftHistory of logicTerm logiccategorical propositionsCategoriesOn Interpretationlogica vetuslogica novaassertoricJohn BuridanmodalizedBoethiusPeter Abelardde dictoJean BuridanaxiomsFrancis BaconPosterior AnalyticsdisjunctiveconditionalImmanuel KantBernard BolzanoBohemiaAustrian Empiresentential logicpredicate logicCongregation for the Doctrine of the FaithRoman RotaGeorge BooleJohn CorcoranLaws of Thoughtvaliditycategorical propositionuniversal propositionsparticular propositionspredicatePolysyllogismsquare of oppositionList of valid argument formscopulainfix operatorsfollow logicallyexistential fallacymedieval SchoolsmnemonicgraphssquaresrectanglesrhombusesVenn diagramssingular termsdistributivesuppositfallacy of the undistributed middledistributionUndistributed middleIllicit treatment of the major termIllicit treatment of the minor termExclusive premisesAffirmative conclusion from a negative premiseNegative conclusion from affirmative premisesDisjunctive syllogismHypothetical syllogismLegal syllogismProsleptic syllogismQuasi-syllogismStatistical syllogismSyllogistic fallacyBuddhist logicEnthymemeFormal fallacyLogical fallacyThe False Subtlety of the Four Syllogistic FiguresTautology (logic)Venn diagramFrede, MichaelBobzien, SusanneStanford Encyclopedia of PhilosophyBacon, FrancisConstitution SocietyBoole, GeorgeThe Laws of ThoughtPrometheus BooksPhilosophy in ReviewCorcoran, JohnPsychological BulletinCognitive PsychologyBlackburn, SimonThe Oxford Dictionary of PhilosophyCopi, IrvingJournal of Symbolic LogicAncient PhilosophyPeter LangHamblin, Charles LeonardMethuenŁukasiewicz, JanHarvard University PressSmiley, TimothyJournal of Philosophical LogicPhilosophiaZalta, Edward N.Aristotelian logicProblem of multiple generalityDictum de omni et nulloSyncategoremaPredicableDefinitionDifferentiaPropertyAccident