Arnold tongue
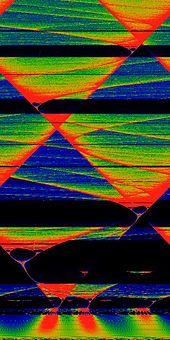
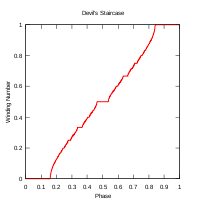
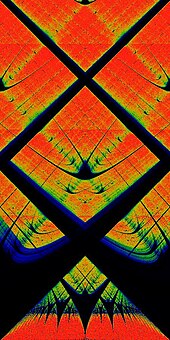
In mathematics, particularly in dynamical systems, Arnold tongues (named after Vladimir Arnold)[1][2] are a pictorial phenomenon that occur when visualizing how the rotation number of a dynamical system, or other related invariant property thereof, changes according to two or more of its parameters.The regions of constant rotation number have been observed, for some dynamical systems, to form geometric shapes that resemble tongues, in which case they are called Arnold tongues.[3] Arnold tongues are observed in a large variety of natural phenomena that involve oscillating quantities, such as concentration of enzymes and substrates in biological processes[4] and cardiac electric waves.Sometimes the frequency of oscillation depends on, or is constrained (i.e., phase-locked or mode-locked, in some contexts) based on some quantity, and it is often of interest to study this relation.For instance, the outset of a tumor triggers in the area a series of substance (mainly proteins) oscillations that interact with each other; simulations show that these interactions cause Arnold tongues to appear, that is, the frequency of some oscillations constrain the others, and this can be used to control tumor growth.[3] Other examples where Arnold tongues can be found include the inharmonicity of musical instruments, orbital resonance and tidal locking of orbiting moons, mode-locking in fiber optics and phase-locked loops and other electronic oscillators, as well as in cardiac rhythms, heart arrhythmias and cell cycle.[5] One of the simplest physical models that exhibits mode-locking consists of two rotating disks connected by a weak spring.One disk is allowed to spin freely, and the other is driven by a motor.Mode locking occurs when the freely-spinning disk turns at a frequency that is a rational multiple of that of the driven rotator.The simplest mathematical model that exhibits mode-locking is the circle map, which attempts to capture the motion of the spinning disks at discrete time intervals.That is, one oscillator depends on the other but not the other way around, so they do not mutually influence each other as happens in Kuramoto models, for example.This is a particular case of driven oscillators, with a driving force that has a periodic behaviour.The family of circle maps serves as a useful mathematical model for this biological phenomenon, as well as many others.is a periodic function that yields the influence caused by the external oscillator.The particular circle map originally studied by Arnold,[8] and which continues to prove useful even nowadays, is: wherewe obtain the circle map discussed previously: Glass, L. (2001) argues that this simple model is applicable to some biological systems, such as regulation of substance concentration in cells or blood, withIn a phase-locked region, the values θn advance essentially as a rational multiple of n, although they may do so chaotically on the small scale.The limiting behavior in the mode-locked regions is given by the rotation number.The phase-locked regions, or Arnold tongues, are illustrated in yellow in the figure to the right.Each such V-shaped region touches down to a rational value Ω = p/q in the limit of K → 0.One reason the term "locking" is used is that the individual values θn can be perturbed by rather large random disturbances (up to the width of the tongue, for a given value of K), without disturbing the limiting rotation number.That is, the sequence stays "locked on" to the signal, despite the addition of significant noise to the series θn.This ability to "lock on" in the presence of noise is central to the utility of the phase-locked loop electronic circuit.[citation needed] There is a mode-locked region for every rational number p/q.The largest tongues, ordered by size, occur at the Farey fractions.Fixing K and taking a cross-section through this image, so that ω is plotted as a function of Ω, gives the "Devil's staircase", a shape that is generically similar to the Cantor function.One can show that for K<1, the circle map is a diffeomorphism, there exist only one stable solution.For the circle map it can be shown that in this region, no more than two stable mode locking regions can overlap, but if there is any limit to the number of overlapping Arnold tongues for general synchronised systems is not known.[citation needed] The circle map also exhibits subharmonic routes to chaos, that is, period doubling of the form 3, 6, 12, 24,....The standard map is studied in physics by means of the kicked rotor Hamiltonian.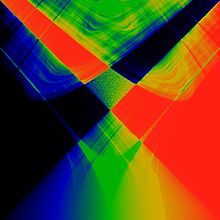
![{\displaystyle [-0.5,0.5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f82e0cb567f3dc7df3709b7077b346272589753)
![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
mathematicsdynamical systemsVladimir Arnoldrotation numberinvariant propertygeometric shapescardiac electric wavesorbital resonancetidal lockingmode-lockingfiber opticsphase-locked loopselectronic oscillatorscardiac rhythmsheart arrhythmiascell cyclerationalBifurcation diagramoscillatorsKuramoto modelsheart cellsartificial pacemakersendomorphismsmoduloirrational rotationperiodic orbitsperiod-doubling bifurcationschaotic behaviorrational multiplewinding numbermeasure zeroFarey fractionsCantor functionsubharmonic routesChirikov standard mapphysicskicked rotorHamiltonianSturmian wordBibcodeCiteSeerXWeisstein, Eric W.MathWorldGlass, L.Chaos theoryAttractorBifurcationFractalLimit setLyapunov exponentPeriodic pointPhase spaceAnosov diffeomorphismaxiom A dynamical systemBox-counting dimensionCorrelation dimensionConservative systemErgodicityFalse nearest neighborsHausdorff dimensionInvariant measureLyapunov stabilityMeasure-preserving dynamical systemMixingPoincaré sectionRecurrence plotSRB measureStable manifoldTopological conjugacyLiouville's theoremKrylov–Bogolyubov theoremPoincaré–Bendixson theoremPoincaré recurrence theoremStable manifold theoremTakens's theoremBifurcation theoryControl of chaosDynamical systemErgodic theoryQuantum chaosStability theorySynchronization of chaosArnold's cat mapBaker's mapComplex quadratic mapCoupled map latticeDuffing mapDyadic transformationDynamical billiardsExponential mapGauss mapGingerbreadman mapHénon mapHorseshoe mapIkeda mapInterval exchange mapKaplan–Yorke mapLangton's antLogistic mapStandard mapTent mapTinkerbell mapZaslavskii mapDouble scroll attractorDuffing equationLorenz systemLotka–Volterra equationsMackey–Glass equationsRabinovich–Fabrikant equationsRössler attractorThree-body problemVan der Pol oscillatorChua's circuitConvectionDouble pendulumElastic pendulumFPUT problemHénon–Heiles systemKicked rotatorMultiscroll attractorPopulation dynamicsSwinging Atwood's machineTilt-A-WhirlWeatherMichael BerryRufus Bowen